Contact dynamics
During the research we deal with the motion of bodies in contact with each other, and with the effect and modeling of friction and impacts
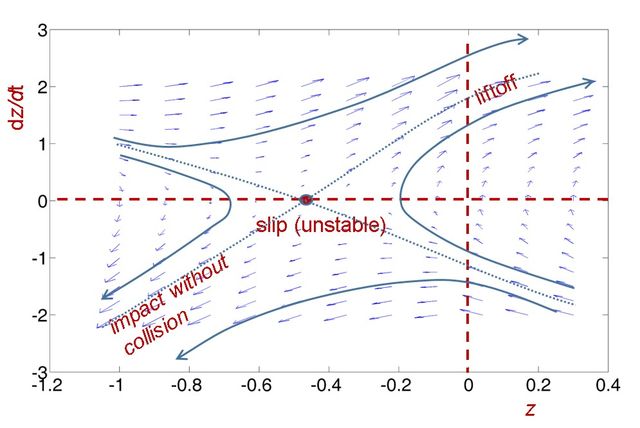
One of our main goals is to understand the singularities that occur during movement, as well as the inconsistency of rigid body models. We have described new cases of the classical Painlevé paradox and found possible resolutions. By examining the motion of slipping objects, we described phenomena in which the contact force diverges to infinity. A new explanation has been given for the singularity that occurs at the terminal point of the motion of a spinning disk: micro-collisions can also explain the observed behavior.
Another central topic is understanding of the stability properties of equilibria under contact. This is a key issue for robotic applications, but there is no generally applicable testing method. We have developed stability conditions applicable to an important model problem: a rigid body with two point contacts.
Links:
[An elective course in contact dynamics]
http://www.szt.bme.hu/files/varkonyi/Kontaktdinamika/index.html
[Our review paper on the Painlevé paradox]
https://arxiv.org/abs/1601.03545
https://youtu.be/w9DbSfjsV9U